Waves & Euler Formulas
Wave functions are typically denoted by the Greek letter psi \(\psi\) and are made up of a spatial frequency variable \(k\) and a variable that represents 1-dimensional space \(x\).
Consider the function for a sine wave \(\psi_{1}\)
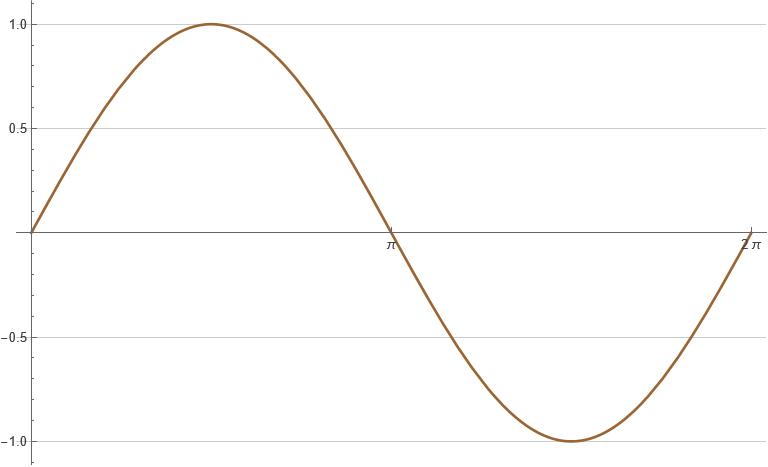
\[\psi_{1} = sin(kx)\]For \(k=1\), the plot of \(\psi_{1}\) from \(x[0,2\pi]\) looks like
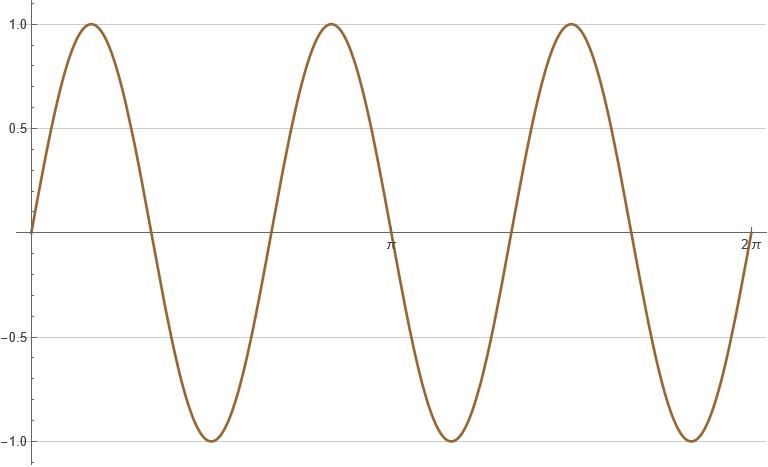
A higher value of \(k\) (say \(k=3\)) changes the plot of \(\psi_{1}\) as such
Waves aren’t only sine waves. Some examples of other wave functions are
\[\begin{align} \psi_{2} & = cos(kx) \\ \psi_{3} & = cos(kx) + isin(kx) \end{align}\]Recall Euler’s Formula
\[e^{ix} = cos(x) + isin(x)\]Thus the above wave functions can be rewritten in terms of their real and imaginary parts:
\[\begin{align} \psi_{1} & = sin(kx) \\ & = \frac{e^{ikx}-e^{-ikx}}{2i} \\ \psi_{2} & = cos(kx) \\ & = \frac{e^{ikx}+e^{-ikx}}{2} \\ \psi_{3} & = cos(kx) + isin(kx) \\ & = e^{ikx} \end{align}\]Page Author: Reagan McNeill Womack